CARATTERISTICHE CHIMICO-FISICHE DEGLI ANESTETICI PER INALAZIONE
Salvo I., Calderini E., Casati A., Fiori R., Torri G.

La conoscenza delle caratteristiche fisico-chimiche degli anestetici per inalazione ha consentito il preciso collocamento clinico di ciascuno di essi e rappresenta oggi la base non solo per l'immediata valutazione di nuovi farmaci, ma anche per poter predire la loro attività ed il loro profilo farmacodinamico.

Nella tabella 1 sono riportate le principali caratteristiche fisico-chimiche degli anestetici volatili che verranno in seguito discusse. L'unico anestetico inalatorio inorganico ancora utilizzato è il protossido d'azoto, quelli organici invece rappresentano una classe eterogenea divisibile in due gruppi: idrocarburi ed eteri, i quali a loro volta possono essere suddivisi in forme semplici e forme alogeno sostituite.

Gli idrocarburi semplici sono il ciclopropano e l'etilene; quelli alogenati comprendono il cloroformio e l'alotano. Fra gli eteri semplici troviamo l'etere divinilico e l'etere dietilico; sono invece eteri alogenati il metossiflurane, l'enflurane, l'isoflurane ed il desflurane (fig 1).

Tabella 1: Principali caratteristiche fisico-chimiche degli anestetici per inalazione

Peso molecolare

La diversità strutturale degli anestetici per inalazione spiega la notevole differenza tra i rispettivi pesi molecolari: la molecola più leggera è quella del ciclopropano (PM = 42,08) composto assai semplice, mentre le molecole più pesanti sono quelle dei moderni anestetici alogeno sostituiti come l'alotano, che contiene tutti e tre gli alogeni ed è la più pesante di tutte (PM = 197,38).

Densità

Se consideriamo una massa di gas in moli ed il volume da essa occupato a pressione e temperatura standard (P.T.S. = 0 °C e 760 mmHg) possiamo calcolare la densità di quel gas,

cioè il peso in grammi di un litro dello stesso gas.

Eseguendo questo calcolo per tre comuni gas anestetici si ottiene :

Protossido d'azoto: 1 mole = 44,01 g; 44,01/22,4 = 1,964 g.l^-1

Isoflurane: 1 mole = 184,5 g ; 184,5/22,4 = 8,263 g.l^-1

Alotano: 1 mole = 197,4 g ; 197,4/22,4 = 8,81 g.l^-1

La densità definita come concentrazione di materia (dimensionalmente massa x lunghezza³) è sinonimo di peso specifico.

La densità relativa è il rapporto tra la densità della sostanza in esame e quella dell'aria, se si tratta di un gas, considerando quest'ultima convenzionalmente uguale a 1 (densità relativa e peso specifico coincidenti); se si tratta di un liquido il secondo termine del rapporto invece di essere l'aria è l'acqua.

Se consideriamo un anestetico di cui è nota la densità (g x ml^-1) allo stato liquido, e conosciamo la densità della sua fase gassosa (g x l^-1), possiamo calcolare quanti milliletri di vapore si ottengono dalla vaporizzazione di un milliletro di anestetico liquido.

Usando come anestetico l'isoflurane si ha:

peso di 1 ml di isoflurane liquido = 1,49 g x ml^-1

peso di 1 l di vapore di isoflurane = 8,25 g x l^-1

8,25/1,49 = 5,5 ml di anestetico che danno origine ad 1 l di vapore

1000/5,5 = 181,8 ml di vapore ottenuti da 1 ml di anestetico liquido

A P.T.S. il calcolo precedente è riassumibile con la formula:

Peso Specifico x 22,4 x 1000 Peso Molecolare

Per gli anestetici gassosi a P.T.S. il calcolo si riferisce alla pressione di liquefazione; per il protossido d'azoto, nota la sua densità (0,8 g x ml^-1) a 20 °C e 51 Kg x cm^-2, e la densità del gas a temperatura ambiente (1,8 g x l^-1) il calcolo è il seguente:

1,8/0,8 = 2,2 1000/2,2 = 450 ml

Evaporazione, ebollizione, volatilità

Il passaggio alla fase gassosa di un anestetico liquido comporta una variazione di stato della materia che richiede un certo lavoro: l'energia utilizzata è quella termica. Se somministriamo calore o lo sottraiamo si ha una variazione di temperatura fino al momento in cui inizia la variazione di stato e per tutta la sua durata.

La variazione di stato assorbe o cede una certa quantità di energia termica o calore latente, esso è caratteristico della sostanza considerata e dipende dalla temperatura del sistema.

Le molecole di cui un liquido è composto sono in uno stato di movimento continuo legato all'energia termica: i loro movimenti sono condizionati dalle collisioni con le molecole vicine e dalle forze di attrazione e repulsione intermolecolari.

Il comportamento delle molecole di un liquido è intermedio tra ciò che avviene nella materia solida dove si hanno solo piccole oscillazioni delle molecole intorno ad un punto fisso, e ciò che avviene in un gas ove le molecole possono percorrere un tragitto centinaia di volte più grande del loro diametro senza collisioni con altre particelle.

A loro volta le molecole del liquido si attraggono con una forza che varia in ragione inversa della settima potenza della distanza che le separa [2] : tali forze di attrazione divengono così considerevoli quando le distanze intermolecolari sono dell'ordine di poco più di un diametro molecolare.

Le principali caratteristiche dei liquidi sono infatti legate a queste potenti forze di coesione.

Le forze di repulsione, pur essendo assai più piccole che nei solidi giacché le distanze tra le molecole sono relativamente più grandi, sono in equilibrio con le forze di repulsione e ciò dà origine alla cosiddetta pressione interna del liquido.

Una molecola sulla superficie di un liquido è sottoposta ad una trazione prevalente verso l'interno del liquido stesso dove il numero di molecole per unità di volume è più elevato. Il superamento di tale forza ed il passaggio dal liquido al vapore è il risultato di un certo numero di collisioni che portano ad un allontanamento delle molecole più cariche di energia; questo fenomeno comporta una perdita di energia, cioè un abbassamento di temperatura, che è rappresentata dal calore latente di evaporazione.

Il calore latente di evaporazione è definito come la quantità di calore necessaria per trasformare un grammo o un millilitro o una mole di liquido in vapore senza variazioni della temperatura, ed è misurato in calorie per grammo o rispettivamente per millilitro o per mole.

Il calore latente di evaporazione varia con la temperatura del liquido in modo inversamente proporzionale. Il numero di calorie necessario per l'evaporazione di una certa quantità di liquido senza variazione di temperatura diminuisce col crescere della temperatura del sistema fino alla temperatura critica, alla quale il calore latente di evaporazione è zero ed il liquido si trasforma in vapore spontaneamente senza assorbimento di ulteriore calore.

Si è rilevato come introducendo in un recipiente chiuso un liquido, o un gas liquefatto al di sotto della temperatura critica, si instauri un equilibrio tra fase liquida e fase gassosa sovrastante: da questo momento la concentrazione delle molecole nel vapore resta costante e dipende solo dalla temperatura, così che il numero di molecole che abbandonano il liquido è uguale al numero di molecole che ritornano nel liquido in un dato tempo. Lo spazio al di sopra del liquido è saturo di vapore e la pressione che questo esercita è la tensione di saturazione del vapore o, più comunemente, la tensione di vapore del liquido ad una data temperatura.

In condizioni identiche di pressione e di temperatura i diversi anestetici liquidi hanno tensioni di vapore diverse. Tanto più elevata è la tensione di vapore e tanto più volatile si definisce l'anestetico.

La curva che esprime l'andamento della tensione di vapore in funzione della temperatura è di tipo logaritmico: tale andamento è calcolabile per ciascun anestetico liquido mediante l'equazione termodinamica di Clapeyron-Clausius , noto il calore latente di evaporazione alle diverse temperature (fig. 2).

Quando la tensione di vapore è uguale alla pressione barometrica , la trasformazione da liquido a vapore si svolge rapidamente anche in seno al liquido stesso, e non solo alla sua superficie, con la formazione di bolle nel liquido; tale cambiamento di stato è chiamato ebollizione ed avviene ad una temperatura caratteristica per ciascun liquido in funzione della pressione barometrica.

Pressione parziale

La teoria cinetica dei gas stabilisce che la pressione di un gas dipende dalla somma degli urti delle sue molecole contro le pareti del recipiente in cui è contenuto, ed è tanto più elevata quanto maggiore è il numero delle molecole stesse e quanto più grande la loro energia potenziale media.

Matematicamente, per un gas ideale, può essere espressa come:

P = NkT / V  
dove

P = pressione esercitata
V = volume in cui è contenuto il gas
k = costante di Boltzman (media di variazione di energia cinetica di una molecola per un au mento di temperatura di 1 °C)
T = temperatura assoluta

Il comportamento della maggior parte dei gas segue quello predetto dalla legge dei gas ideali.

Se invece di un solo gas abbiamo una miscela di gas, la pressione totale è data dalla somma delle pressioni parziali dei singoli gas componenti la miscela (legge di Dalton), definendo come

pressione parziale quella che ciascun gas eserciterebbe se occupasse da solo il volume occupato dalla miscela alla stessa temperatura.

Per ogni gas la legge dei gas ideali può essere riscritta separatamente:

P₁ x V = N₁ x k x T

La somma delle pressioni parziali, secondo la legge di Dalton , è uguale alla pressione totale(P):

P x V = (P₁+P₂+....) x V = (N₁+N₂+...) x kT = NkT

Dividendo la precedente equazione per quest'ultima si ottiene: 

P₁/P = N₁/N

Per quanto detto e per la legge di Avogadro, in condizioni costanti di pressione e temperatura, il numero di molecole gassose contenute nel recipiente è costante ed indipendente dalla natura del gas e dal fatto che si tratti di una miscela invece che di un unico gas.

Figura 2 - Tensione di vapore di alcuni anestetici in funzione della temperatura

Ciascun componente la miscela esercita una pressione che ha lo stesso rapporto con la pressione totale che ha il volume occupato dal gas rispetto al volume totale del recipiente. La pressione parziale di un gas è un dato di estrema importanza: dal suo valore dipende la diffusione delle molecole, queste infatti tendono a diffondere da una regione dove la pressione parziale è maggiore a una dove la pressione parziale è minore, tendendo al raggiungimento dell'equilibrio.
Il problema della diffusione di un gas in un liquido è regolato anch'esso dalla pressione parziale del gas. Per la legge di Henry la quantità di gas disciolta in un liquido ad una data temperatura è proporzionale alla pressione parziale del gas nella fase gassosa. Se il gas disciolto non è costituito da una sola sostanza ma è una miscela, la legge di Henry si applica ad ogni componente indipendentemente dalla pressione degli altri. A saturazione quindi ciascun gas esercita nel liquido una tensione che è convenzionalmente uguale alla sua pressione parziale nella miscela gassosa in equilibrio con il liquido. L'equilibrio è raggiunto quando il numero di molecole che passa dalla fase gassosa a quella liquida è uguale al numero di molecole che dalla fase liquida passa a quella gassosa. A parità di pressione parziale la concentrazione di un gas nella fase liquida può essere molto diversa in quanto dipende dalla solubilità del gas nel liquido in questione.

Solubilità

Tutti i gas sono solubili nei liquidi. Tale solubilità è limitata e dipende dalla natura del gas e del liquido, dalla temperatura e dalla pressione. La quantità di gas che si scioglie in un liquido è direttamente proporzionale alla pressione del gas (legge di Henry) ed inversamente proporzionale alla temperatura del liquido. La solubilità di un gas in un liquido può essere espressa mediante due coefficienti : quello di Bunsen e quello di Ostwald.

Il coefficiente di assorbimento ( di Bunsen) è definito come il volume di gas, ridotto a P.T.S., disciolto nell'unità di volume del liquido alla temperatura sperimentale e alla pressione parziale del gas di 760 mm Hg.
Matematicamente: coefficiente di Bunsen

a = v/V x p

v = volume di gas sciolto ridotto a P.T.S.
V = volume del liquido solvente
p = pressione parziale del gas.

Il coefficiente di solubilità (di Ostwald) è definito come il volume di gas, misurato a P.T.S., sciolto nell'unità di volume di liquido: coefficiente di Ostwald

b = v/V

v = volume effettivo di gas disciolto misurato alla temperatura sperimentale T ed alla pressione parziale p.

Come già accennato, il fattore che influenza maggiormente la solubilità di un gas è la pressione e secondariamente la temperatura.

La relazione quantitativa tra solubilità e pressione è espressa dalla legge di Henry : la massa di gas disciolta in un dato volume di liquido solvente a pressione costante è direttamente proporzionale alla pressione del gas in equilibrio con il liquido.

Matematicamente questa relazione può essere espressa come:

m = k x p

m = massa del gas disciolta per unità di volume di liquido alla pressione di equilibrio p
k = costante di proporzionalità.

La relazione precedente ci dice che all'aumento della pressione del gas sovrastante il liquido la massa di gas disciolta aumenta proporzionalmente. Il volume di gas disciolto, misurato alla pressione di esperienza , è indipendente dalla pressione . Il volume occupato da una certa massa di gas è, secondo la legge di Boyle, inversamente proporzionale alla pressione, così che, se aumenta la massa di gas proporzionalmente alla pressione, il volume deve rimanere costante.

Da quanto detto si ricava che il coefficiente di solubilità di Ostwald, a temperatura definita, deve essere indipendente dalla pressione e questo è quello che si verifica sperimentalmente.

La legge di Henry può essere espressa in un altro modo assai semplice che permette di introdurre il concetto di coefficiente di ripartizione.

La massa m di un gas disciolto per unità di volume di liquido corrisponde alla concentrazione in g x ml^-1 (che è a sua volta proporzionale alla concentrazione in moli l^-1 di liquido) poiché non vi è sensibile variazione di volume quando il gas si scioglie.

La concentrazione in moli per litro di gas è proporzionale alla pressione e viceversa.

Sapendo che il rapporto m/p è costante, possiamo scrivere che il rapporto:

Concentrazione gas fase liquida / concentrazione fase gassosa = costante

per una certa temperatura ed è indipendente dalla pressione. L'equazione precedente costituisce la legge di ripartizione ed il rapporto viene definito coefficiente di ripartizione, indicato con la lettera l . La legge così espressa si riferisce alla ripartizione del gas tra uno spazio libero ed un liquido secondo un rapporto costante. La legge può essere inoltre applicata a qualsiasi sistema a due fasi: per esempio due liquidi non miscibili , o un liquido ed un solido (sangue/tessuti o sangue/liquor) quando si aggiunga a tale sistema una terza sostanza miscibile con entrambi (ad esempio un anestetico per inalazione), stabilendo che tale sostanza si distribuirà tra le due fasi in modo definito, dipendente dalla temperatura ed indipendente dalla quantità totale di sostanza disciolta. Il coefficiente di ripartizione, come rapporto di concentrazioni, è dimensionalmente un numero puro. Esso è certamente l'indice più significativo nello studio di un anestetico per inalazione dal punto di vista del suo comportamento nell'organismo umano: più del dato assoluto di solubilità la farmacocinetica di un gas nell'organismo utilizza dati relativi, essendo l'organismo costituito da sistemi binari a due fasi (sangue/gas e tessuto/sangue) (tab. 2).

Il coefficiente di ripartizione sangue/gas ha una precisa correlazione con la durata della fase di induzione e di quella di risveglio di una narcosi : quanto più elevato è il coefficiente di ripartizione sangue/gas, tanto maggiore è la quantità di anestetico che, a parità di pressione parziale in fase gassosa, si scioglie nel sangue [3].

Tabella 2 - Coefficienti di ripartizione sangue/gas di alcuni anestetici per inalazione calcolati a 37 °C

Cinque variabili influenzano il coefficiente di ripartizione sangue/gas :

1. l'anestetico

2. la temperatura

3. i costituenti plasmatici

4. l'ematocrito

5. l'età.

Il rapporto tra solubilità e temperatura è assai semplice: ad un aumento di temperatura corrisponde una diminuzione della solubilità del gas. A questa regola fanno eccezione solo alcuni gas poco solubili (idrogeno e gas inerti) che dimostrano un comportamento speciale [4,5,6]. L'importanza di queste variazioni del coefficiente di ripartizione sangue/gas nella pratica clinica , dove l'ipotermia modesta in corso di intervento chirurgico in anestesia generale è un'evenienza abbastanza comune, è grande: la quantità di anestetico che si scioglie nel torrente ematico a temperature inferiori alla norma è maggiore ed aumenta quindi la capacità nell'intero organismo per gli anestetici.

Tabella 3 - Coefficiente di ripartizione sangue/gas di alcuni anestetici a tre diverse temperature

Un altro fattore che influenza il coefficiente di ripartizione sangue/gas degli anestetici per inalazione è la composizione del sangue [6.7]

Gli anestetici per inalazione tendono a formare legami con i gruppi polari delle proteine ematiche e soprattutto delle albumine. La diminuzione di solubilità con la diminuzione della quota proteica o il suo aumento in opposte condizioni sono per gli anestetici più solubili di entità assai elevate e pari a quelle che si osservano in ipotermia. E' inoltre noto come per enflurane, alotano ed isoflurane i coefficienti di ripartizione sangue/gas si modifichino parallelamente alle variazioni di ematocrito e dei costituenti plasmatici. All'aumento dell'ematocrito il coefficiente di ripartizione sangue/gas dell'isoflurane diminuisce in maniera lineare, mentre quello dell'enflurane aumenta linearmente; per gli altri anestetici inalatori (alotano, metossiflurane) le variazioni dell'ematocrito non hanno indotto una variazione del coefficiente di ripartizione [8,9].

Anche l'età influenza significativamente la solubilità degli anestetici inalatori [10,11]. Si è notato un incremento della solubilità degli anestetici per inalazione con l'avanzare dell'età fino all'età adulta, per poi ridiscendere gradualmente nell'anziano e grande anziano. Il coefficiente di ripartizione sangue/gas è per l'isoflurane di 1,19 nei neonati, 1,28 nei bambini e 1,46 negli adulti. Per l'alotano nei medesimi gruppi di età il coefficiente di ripartizione sangue/gas è: 2,14 ; 2,9; 2,64 (fig. 4). Queste variazioni di solubilità si correlano con le differenze di composizione serica, soprattutto per quanto riguarda albumine e trigliceridi, rilevate nei gruppi d'età.

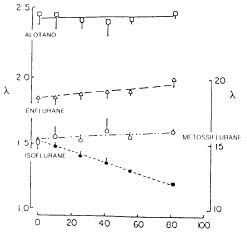Figura 3 - Relazione tra coefficiente di ripartizione sangue / gas ed ematocrito (da Lerman et al.,1984) [8]

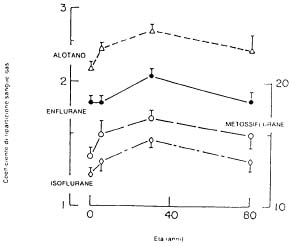Figura 4 - Relazione esistente tra coefficiente di ripartizione sangue/gas ed età (da Lerman et al.,1984) [11]

Diffusione degli anestetici

La diffusione dei gas inerti e degli anestetici per inalazione in un mezzo segue la legge di Fick:

dQ/dt = -A Cd (dG/dx)

dove:

dQ/dt = quantità di sostanza che diffonde nel tempo dt
G = concentrazione del gas
A = area della superficie di scambio
x = distanza interessata dagli scambi
Cd = costante di diffusione (cm²/sec)

Nel caso degli anestetici per inalazione la legge di Fick viene più convenientemente impiegata sostituendo la concentrazione del gas G con un termine che rappresenti anche l'attività che sostiene il fenomeno della diffusione.

Se si considerano due fasi in cui l'anestetico ha differente solubilità il gas può paradossalmente diffondere da quella a minor concentrazione a quella in cui l'anestetico è presente a concentrazione più elevata fino a che non si è stabilito un equilibrio in pressione parziale tra le due fasi.

La pressione parziale di un gas diventa così l'espressione più diretta del fattore che sostiene il processo di diffusione. La concentrazione di un gas in un liquido può essere espressa dal prodotto della sua pressione parziale P per il coefficiente di solubilità di Bunsen (a) nel liquido stesso: sostituendo G nella formula con P si ottiene: 

dQ/dt = - aCd A (dP/dx)

La costante di diffusione in questo caso diventa Cd: in altre parole la costante di diffusione, quando il gradiente di diffusione è la pressione parziale del gas , comprende anche la solubilità del gas nel sistema [12].

Diffusione degli anestetici attraverso la membrana alveolo-capillare : capacità di diffusione degli anestetici

Negli studi di farmacocinetica degli anestetici si è sempre presupposto, omologando il comportamento di questi a quello dei gas inerti, che l'equilibrio in pressione parziale a livello della membrana alveolo-capillare (spessore 0,2 - 0,4 m) sia estremamente rapido e si stabilizzi in un tempo inferiore a quello impiegato dal sangue ad attraversare il capillare polmonare (0,7 sec) . La legge che regola l'equilibrio, in pressione parziale, tra gas contenuto nell'alveolo e gas presente nel capillare polmonare è espressa dalla seguente relazione [13]:
P_A-P_C / P_A-P_C° = e 760 D_M / a_sV_C⁶⁰ X t
dove
D_M = capacità di diffusione del gas attraverso la membrana alveolo-capillare (in ml di gas/min/mmHg)
a_s = solubilità del gas nel sangue (coeff.di Bunsen)
V_C = volume del capillare polmonare
t = tempo in secondi.

Il valore di D_M, secondo la legge di Graham, è direttamente proporzionale alla solubilità del gas nel mezzo ed inversamente proporzionale alla radice quadrata del peso molecolare.

E' stato dimostrato (Torri e Damia, 1969) come la velocità di equilibrazione tra pressione parziale a livello alveolare e nel sangue capillare sia un fenomeno rapido e come nel 99% dei casi si realizzi in un tempo notevolmente inferiore a quello impiegato dal sangue ad attraversare il capillare polmonare.

Se al termine del capillare polmonare la pressione parziale dell'anestetico è la stessa del gas alveolare possiamo conoscere la sua concentrazione arteriosa una volta che siano noti concentrazione alveolare e coefficiente di ripartizione sangue/gas.

Diffusione degli anestetici dai capillari ai tessuti

Gli scambi gassosi tra sangue capillare e tessuto sono molto più complessi rispetto agli scambi a livello alveolare: ciò dipende dal fatto che con ogni probabilità la diffusione a livello tessutale trova alcuni limiti.

Kety e coll. hanno determinato la concentrazione di protossido d'azoto in prelievi di tessuto cerebrale e nel sangue refluo dall'encefalo [15]. Essi hanno constatato che encefalo e sangue venoso refluo erano in equilibrio durante la fase di assorbimento del gas fatta eccezione per i

primi quattro minuti. Ciò potrebbe dipendere dalla non uniforme distribuzione dei capillari nel tessuto cerebrale o dalla impossibilità di avere un completo equilibrio nei singoli capillari.

La velocità con cui si stabilisce un equilibrio tra capillare e tessuto circostante dipende certamente da due fattori: il diametro interno del capillare ed il numero di capillari presenti nell'unità di volume del tessuto.

Secondo Forster [12] l'equilibrio in pressione parziale di un anestetico fra sangue capillare e tessuto circostante è totale solo nei tessuti ad elevata perfusione (encefalo, rene, fegato e miocardio) mentre è solo parziale in quelli a bassa perfusione quali i muscoli ed il tessuto adiposo.

BIBLIOGRAFIA

1. Handbook Chem. Phys. 1968/69

2. Glasstone S.: Textbook of phisycal chemistry. Ed C. Manfredi, Milano, 1959

3. Lowe H.J. , Hagler K. : Determination of volatile organic anaesthetics in blood, gases, tissue and lipids: parition coefficients. In Gaschromatography in biology and medecine R. Poster, Ed. Churchill,London,1969

4. Eger R., Eger E.I.: Effect of temperature and age on the solubility of enflurane, halothane, isoflurane and methoxyflurane in human blood. Aneth. Anlg.,64,640,1985

5. Han Y., Helrich M.,et all.: Effect of temperature on solubility of halothane in human blood and brain tissue homogenate. Anesth. Analg., 45,755,1966

6. Laasberg L. et all.: Halothane solubility in blood and solutions of plasms proteins: effect of temperature, protein composition, and hemoglobin concentration. Anesthesiology, 32, 351, 1970

7. Frova G. , Torri G., et all.: Solubilità degli anestetici a differenti valori di ematocrito. Com. XXII Congr. SIAR, Firenze,1970

8. Lerman J., Gregory G., et all. : Hematocrit and solubility of volatile anesthetics in blood. Anesth. Analg.,63,911,1984

9. Lerman J., Gregory G.,et all. : Effects of anaesthesia and surgery on the solubility of volatile anesthetics in blood Can. J. Anaesth.,34,14,1987

10. Lerman J., Schmitt-Bantel B.,et all: Effect of age on the solubility of volatile anesthetics in human tissues. Anesthesiology,65,307,1986

11. Lerman J ., Gregory G., et all.: Age and solubility of volatile anesthetics in blood. Anesthesiology,61,139,1984

12. Forster R.E. : Diffusion factors in gases and liquids. Cap. 2 in : Uptake and distribution of anesthetic agents. EM Papper and JR Kitz Editors. Mc Kraw-Hill, N.Y. 1963

13. Forster R.E.: Exchange of gases between alveolar air and pulmonary capillary blood: pulmonary diffusing capacity. Physiol. Rev.,37,391,1957

14. Torri G., Damia G.: Diffusione degli anestetici per inalazione attraverso la membrana alveolo-capillare. Anest. Rianim.,10,189,1969

15. Kety S.,Harnell H. et all.: The solubility of nitrous oxide in blood and brain. J. Biol. Dem.,173,478,1948